Osorno Jiménez, César. Planeación Didáctica

CENTRO DE ESTUDIOS AVANZADOS DE LAS AMERICAS

MAESTRÍA EN: Ciencias de la Educación

ASIGNATURA: Didáctica y sus recursos

CUATRIMESTRE: 2°

CASO PRÁCTICO

TÍTULO: Planeación didáctica

NOMBRE DEL ALUMNO: Cesar Osorno Jiménez

MATRÍCULA: M24010409070

ASESOR: Mtra. Ruth González Hernández

FECHA: 21 de marzo de 2024

Escuela Secundaria Técnica No. 4 “José Agustín Arrieta” Chiautempan, Tlaxcala Matemáticas I
Docente:	Cesar Osorno Jiménez
Objetivo:	Los alumnos determinan la expresión algebraica de sucesiones con progresión aritmética sencillas.
Contenido:	Regularidades y patrones
Recursos:	Libreta, lápiz, goma, pinturas, regla o escuadra, proyector, video, pizarrón, plumones y laptop

Sucesiones

Intención didáctica: Los alumnos determinan la expresión algebraica de sucesiones con progresión aritmética sencillas.

Indicaciones generales: Encuentra la solución de los siguientes ejercicios que realizaras en tu libreta. Considera cumplir las características solicitadas en la lista de cotejo para que alcances la máxima calificación.

Inicio

(Tiempo estimado: 20 minutos)

Método inductivo   

1) En equipos de tres personas, encuentra el valor desconocido en cada sucesión. Posteriormente con ayuda del profesor comparte tus respuestas con el grupo.

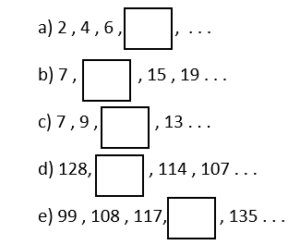
Una sucesión matemática es una secuencia ordenada de números, con determinada relación entre números consecutivos. A cada uno de los números de la sucesión se les denomina términos y se diferencian por su posición (n).

Desarrollo

(Tiempo estimado: 65 minutos)

(Método inductivo)

En equipo de tres personas, soluciona los siguientes desafíos de sucesiones. Al finalizar, un integrante del equipo compartirá las respuestas con sus compañeros en plenaria.

2) Dibuja la figura 5 de la siguiente sucesión y posteriormente completa la tabla.

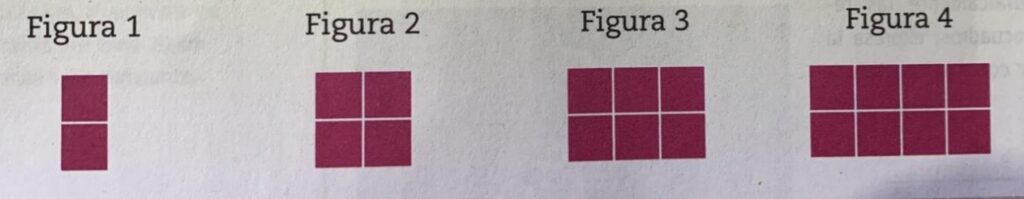
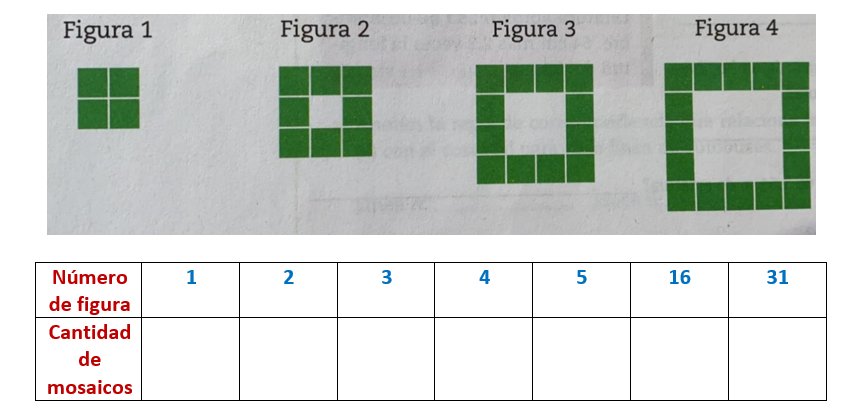
3) Dibuja la figura 5 de la siguiente sucesión y posteriormente completa la tabla.

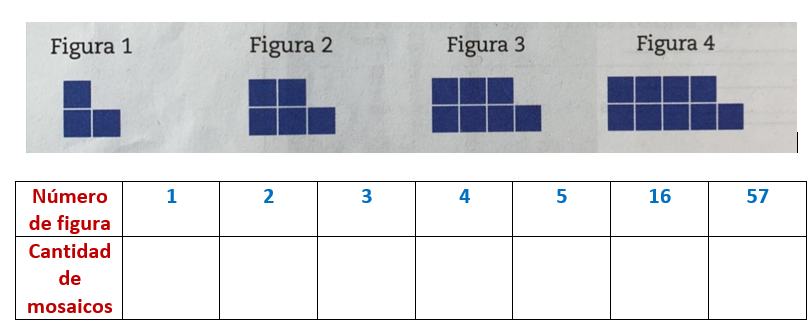
4) Dibuja la figura 5 de la siguiente sucesión y posteriormente completa la tabla.

5) Observa la siguiente sucesión y posteriormente completa la tabla.

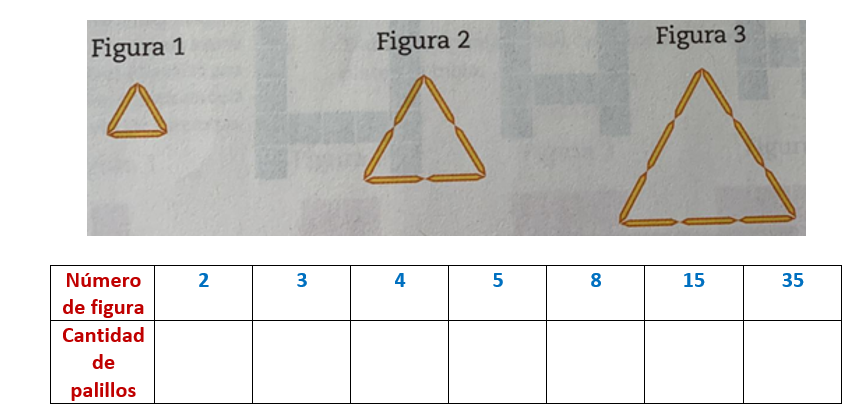
a) ¿Qué operaciones realizaste para encontrar la cantidad de palillos en la figura número 15?

b) ¿Qué operaciones realizaste para encontrar la cantidad de palillos en la figura número 35?

c) ¿Crees que este patrón de operaciones sirva para encontrar la cantidad de palillos necesarios para construir cualquier número de figura, de esta sucesión? ¿Por qué?

d) ¿Cómo expresarías esta generalidad a partir del número de figura de la sucesión?

e) Determina la expresión para calcular el número de palillos a partir del número de figura algebraicamente (utilizando la letra n que representa el número de figura).

f) Observa el siguiente video: https://youtu.be/FGoSqeFl5zg?si=pGqoeSVmzrLyODUf

6) Escribe una regla para calcular la cantidad de mosaicos a partir del número de figura de las sucesiones de las tablas anteriores, observa el ejemplo.

Número de sucesión	Regla para calcular la cantidad de mosaicos a partir del número de figura (n)	Expresión algebraica
2
3
4
5	Se multiplica el número de figura deseada por tres	3n

Cuando se usan letras, como “n”, para representar números, no se emplea el signo x para indicar multiplicación porque puede confundirse con la letra (x). En lugar de escribir 3 x n, se anota 3n, que significa “tres por n” o “tres veces n”.

Cierre

(Tiempo estimado 35 minutos)

Método deductivo

7) Individualmente completa la siguiente tabla y posteriormente responde. Al finalizar con ayuda del profesor compara y comparte tus respuestas con el grupo.

Número de figura	1	2	3	4	6	20	60	n
Cantidad de rombos
Cantidad de triángulos
Total de polígonos

a) Una figura de sucesión G tiene en total 101 polígonos, ¿cuántos rombos tiene? ¿y cuántos triángulos?

Evaluación

Lista de cotejo de trabajo individual
Alumno:
Número de lista:		Grado y grupo:
Indicaciones:	Marca en la escala estimativa el rango que a juicio del evaluador corresponda a cada aspecto. La escala “Bien” corresponde a un punto, la escala “Suficiente” corresponde a 0.5 puntos y la escala “Insuficiente” corresponde a cero puntos. Después de ser llenada la lista de cotejo, se mostrará al alumno para su revisión y retroalimentación.
Aspecto a evaluar		Bien	Suficiente		Insuficiente
1) Sus apuntes están en limpio y ordenados.
2) Sus tablas las realiza con regla, presentables y con trazos limpios.
3) Sus sucesiones las realiza correctamente e iluminadas.
4) Incluye operaciones y procedimientos completos en su libreta.
5) Soluciona o intenta solucionar todos los ejercicios o problemas.
6) Logra encontrar la regla general de una sucesión con progresión aritmética de forma autónoma.
7) Participa activamente con propuestas en su equipo.
8) Respeta las ideas de sus compañeros de grupo.
9) Pone atención a la participación de los otros equipos en la puesta en común de resolución de ejercicios.
10) El alumno entrega los ejercicios en el tiempo indicado.
Subtotal:
Calificación total:

Fuente de consulta:

Jerez, H. (1997). «Pedagogía esencial», México, Editorial Jertalhum.

213-257

Daniel Carreón. (2016, 25 julio). SUCESIONES  Super facil [Vídeo]. YouTube. https://www.youtube.com/watch?v=FGoSqeFl5zg

Block, D., & García, S., Balbuena H., (2018). Conecta Más Matemáticas, SM

 

Bibliografía
Osorno Jiménez, César. Planeación Didáctica. México: CEAAMER, 2024. 6 hojas.